ExpectileGAM¶
from pygam import ExpectileGAM
from pygam.datasets import mcycle
X, y = mcycle(return_X_y=True)
# lets fit the mean model first by CV
gam50 = ExpectileGAM(expectile=0.5).gridsearch(X, y)
# and copy the smoothing to the other models
lam = gam50.lam
# now fit a few more models
gam95 = ExpectileGAM(expectile=0.95, lam=lam).fit(X, y)
gam75 = ExpectileGAM(expectile=0.75, lam=lam).fit(X, y)
gam25 = ExpectileGAM(expectile=0.25, lam=lam).fit(X, y)
gam05 = ExpectileGAM(expectile=0.05, lam=lam).fit(X, y)
from matplotlib import pyplot as plt
XX = gam50.generate_X_grid(term=0, n=500)
plt.scatter(X, y, c='k', alpha=0.2)
plt.plot(XX, gam95.predict(XX), label='0.95')
plt.plot(XX, gam75.predict(XX), label='0.75')
plt.plot(XX, gam50.predict(XX), label='0.50')
plt.plot(XX, gam25.predict(XX), label='0.25')
plt.plot(XX, gam05.predict(XX), label='0.05')
plt.legend()
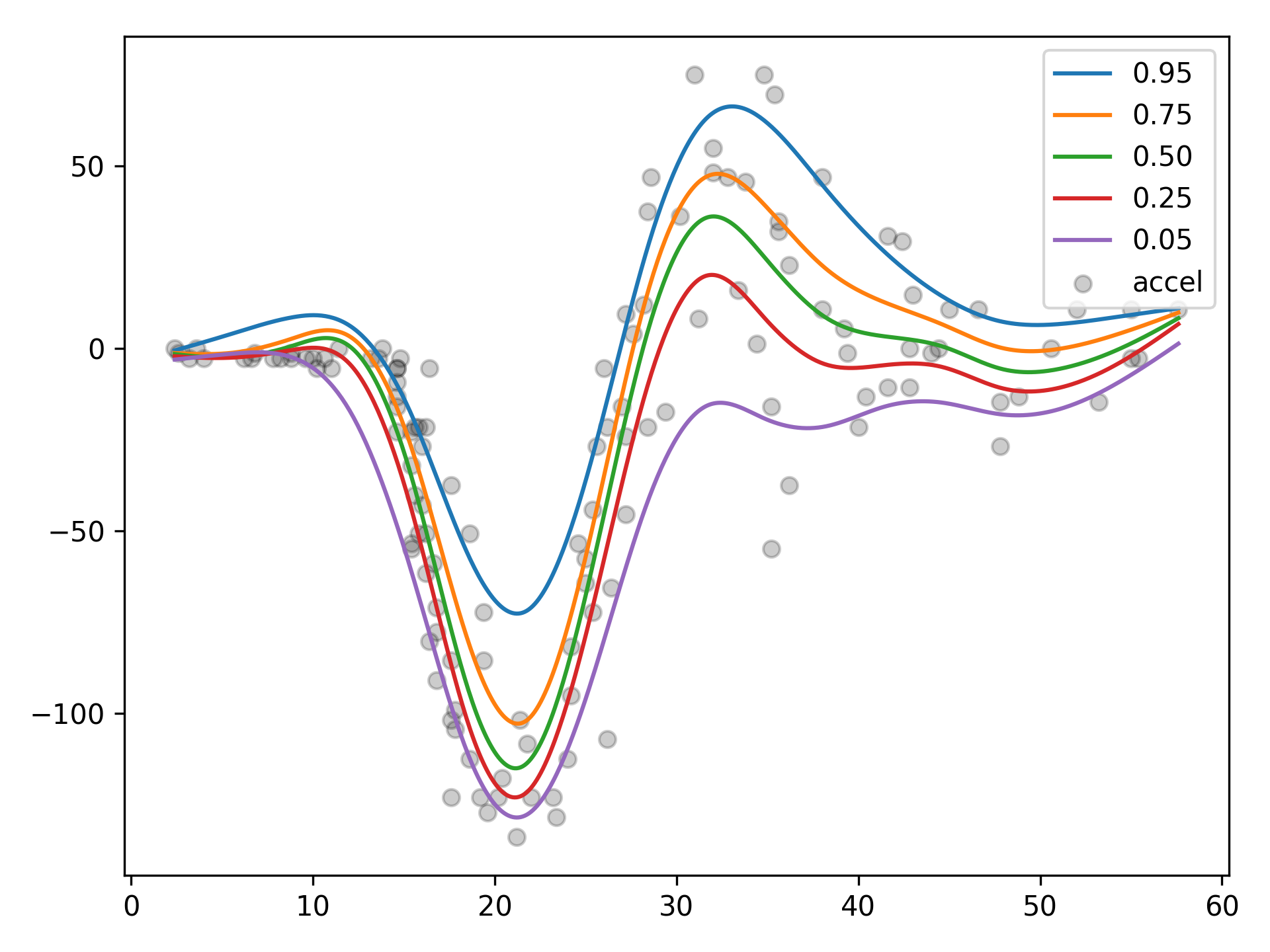
-
class
pygam.pygam.ExpectileGAM(terms='auto', max_iter=100, tol=0.0001, scale=None, callbacks=['deviance', 'diffs'], fit_intercept=True, expectile=0.5, verbose=False, **kwargs)¶ Bases:
pygam.pygam.GAMExpectile GAM
This is a GAM with a Normal distribution and an Identity Link, but minimizing the Least Asymmetrically Weighted Squares
Parameters: - terms (expression specifying terms to model, optional.) –
By default a univariate spline term will be allocated for each feature.
For example:
>>> GAM(s(0) + l(1) + f(2) + te(3, 4))
will fit a spline term on feature 0, a linear term on feature 1, a factor term on feature 2, and a tensor term on features 3 and 4.
- callbacks (list of str or list of CallBack objects, optional) – Names of callback objects to call during the optimization loop.
- fit_intercept (bool, optional) – Specifies if a constant (a.k.a. bias or intercept) should be added to the decision function. Note: the intercept receives no smoothing penalty.
- max_iter (int, optional) – Maximum number of iterations allowed for the solver to converge.
- tol (float, optional) – Tolerance for stopping criteria.
- verbose (bool, optional) – whether to show pyGAM warnings.
-
coef_¶ Coefficient of the features in the decision function. If fit_intercept is True, then self.coef_[0] will contain the bias.
Type: array, shape (n_classes, m_features)
-
statistics_¶ Dictionary containing model statistics like GCV/UBRE scores, AIC/c, parameter covariances, estimated degrees of freedom, etc.
Type: dict
-
logs_¶ Dictionary containing the outputs of any callbacks at each optimization loop.
The logs are structured as
{callback: [...]}Type: dict
References
Simon N. Wood, 2006 Generalized Additive Models: an introduction with R
Hastie, Tibshirani, Friedman The Elements of Statistical Learning http://statweb.stanford.edu/~tibs/ElemStatLearn/printings/ESLII_print10.pdf
Paul Eilers & Brian Marx, 2015 International Biometric Society: A Crash Course on P-splines http://www.ibschannel2015.nl/project/userfiles/Crash_course_handout.pdf
-
confidence_intervals(X, width=0.95, quantiles=None)¶ estimate confidence intervals for the model.
Parameters: - X (array-like of shape (n_samples, m_features)) – Input data matrix
- width (float on [0,1], optional) –
- quantiles (array-like of floats in (0, 1), optional) – Instead of specifying the prediciton width, one can specify the
quantiles. So
width=.95is equivalent toquantiles=[.025, .975]
Returns: intervals
Return type: np.array of shape (n_samples, 2 or len(quantiles))
Notes
- Wood 2006, section 4.9
- Confidence intervals based on section 4.8 rely on large sample results to deal with non-Gaussian distributions, and treat the smoothing parameters as fixed, when in reality they are estimated from the data.
-
deviance_residuals(X, y, weights=None, scaled=False)¶ method to compute the deviance residuals of the model
these are analogous to the residuals of an OLS.
Parameters: - X (array-like) – Input data array of shape (n_samples, m_features)
- y (array-like) – Output data vector of shape (n_samples,)
- weights (array-like shape (n_samples,) or None, optional) – Sample weights. if None, defaults to array of ones
- scaled (bool, optional) – whether to scale the deviance by the (estimated) distribution scale
Returns: deviance_residuals – with shape (n_samples,)
Return type: np.array
-
fit(X, y, weights=None)¶ Fit the generalized additive model.
Parameters: - X (array-like, shape (n_samples, m_features)) – Training vectors.
- y (array-like, shape (n_samples,)) – Target values, ie integers in classification, real numbers in regression)
- weights (array-like shape (n_samples,) or None, optional) – Sample weights. if None, defaults to array of ones
Returns: self – Returns fitted GAM object
Return type:
-
fit_quantile(X, y, quantile, max_iter=20, tol=0.01, weights=None)¶ fit ExpectileGAM to a desired quantile via binary search
Parameters: - X (array-like, shape (n_samples, m_features)) – Training vectors, where n_samples is the number of samples and m_features is the number of features.
- y (array-like, shape (n_samples,)) – Target values (integers in classification, real numbers in regression) For classification, labels must correspond to classes.
- quantile (float on (0, 1)) – desired quantile to fit.
- max_iter (int, default: 20) – maximum number of binary search iterations to perform
- tol (float > 0, default: 0.01) – maximum distance between desired quantile and fitted quantile
- weights (array-like shape (n_samples,) or None, default: None) – containing sample weights if None, defaults to array of ones
Returns: self
Return type: fitted GAM object
-
generate_X_grid(term, n=100, meshgrid=False)¶ create a nice grid of X data
array is sorted by feature and uniformly spaced, so the marginal and joint distributions are likely wrong
if term is >= 0, we generate n samples per feature, which results in n^deg samples, where deg is the degree of the interaction of the term
Parameters: Returns: if meshgrid is False – np.array of shape (n, n_features) where m is the number of (sub)terms in the requested (tensor)term.
else – tuple of len m, where m is the number of (sub)terms in the requested (tensor)term.
each element in the tuple contains a np.ndarray of size (n)^m
Raises: ValueError : – If the term requested is an intercept since it does not make sense to process the intercept term.
-
get_params(deep=False)¶ returns a dict of all of the object’s user-facing parameters
Parameters: deep (boolean, default: False) – when True, also gets non-user-facing paramters Returns: Return type: dict
-
gridsearch(X, y, weights=None, return_scores=False, keep_best=True, objective='auto', progress=True, **param_grids)¶ Performs a grid search over a space of parameters for a given objective
Warning
gridsearchis lazy and will not remove useless combinations from the search space, eg.>>> n_splines=np.arange(5,10), fit_splines=[True, False]
will result in 10 loops, of which 5 are equivalent because
fit_splines = FalseAlso, it is not recommended to search over a grid that alternates between known scales and unknown scales, as the scores of the candidate models will not be comparable.
Parameters: - X (array-like) – input data of shape (n_samples, m_features)
- y (array-like) – label data of shape (n_samples,)
- weights (array-like shape (n_samples,), optional) – sample weights
- return_scores (boolean, optional) – whether to return the hyperpamaters and score for each element in the grid
- keep_best (boolean, optional) – whether to keep the best GAM as self.
- objective ({'auto', 'AIC', 'AICc', 'GCV', 'UBRE'}, optional) – Metric to optimize. If auto, then grid search will optimize GCV for models with unknown scale and UBRE for models with known scale.
- progress (bool, optional) – whether to display a progress bar
- **kwargs –
pairs of parameters and iterables of floats, or parameters and iterables of iterables of floats.
If no parameter are specified,
lam=np.logspace(-3, 3, 11)is used. This results in a 11 points, placed diagonally across lam space.If grid is iterable of iterables of floats, the outer iterable must have length
m_features. the cartesian product of the subgrids in the grid will be tested.If grid is a 2d numpy array, each row of the array will be tested.
The method will make a grid of all the combinations of the parameters and fit a GAM to each combination.
Returns: - if
return_scores=True– model_scores: dict containing each fitted model as keys and corresponding objective scores as values - else – self: ie possibly the newly fitted model
Examples
For a model with 4 terms, and where we expect 4 lam values, our search space for lam must have 4 dimensions.
We can search the space in 3 ways:
1. via cartesian product by specifying the grid as a list. our grid search will consider
11 ** 4points:>>> lam = np.logspace(-3, 3, 11) >>> lams = [lam] * 4 >>> gam.gridsearch(X, y, lam=lams)
2. directly by specifying the grid as a np.ndarray. This is useful for when the dimensionality of the search space is very large, and we would prefer to execute a randomized search:
>>> lams = np.exp(np.random.random(50, 4) * 6 - 3) >>> gam.gridsearch(X, y, lam=lams)
3. copying grids for parameters with multiple dimensions. if we specify a 1D np.ndarray for lam, we are implicitly testing the space where all points have the same value
>>> gam.gridsearch(lam=np.logspace(-3, 3, 11))
is equivalent to:
>>> lam = np.logspace(-3, 3, 11) >>> lams = np.array([lam] * 4) >>> gam.gridsearch(X, y, lam=lams)
-
loglikelihood(X, y, weights=None)¶ compute the log-likelihood of the dataset using the current model
Parameters: - X (array-like of shape (n_samples, m_features)) – containing the input dataset
- y (array-like of shape (n,)) – containing target values
- weights (array-like of shape (n,), optional) – containing sample weights
Returns: log-likelihood – containing log-likelihood scores
Return type: np.array of shape (n,)
-
partial_dependence(term, X=None, width=None, quantiles=None, meshgrid=False)¶ Computes the term functions for the GAM and possibly their confidence intervals.
if both width=None and quantiles=None, then no confidence intervals are computed
Parameters: - term (int, optional) – Term for which to compute the partial dependence functions.
- X (array-like with input data, optional) –
if meshgrid=False, then X should be an array-like of shape (n_samples, m_features).
if meshgrid=True, then X should be a tuple containing an array for each feature in the term.
if None, an equally spaced grid of points is generated.
- width (float on (0, 1), optional) – Width of the confidence interval.
- quantiles (array-like of floats on (0, 1), optional) – instead of specifying the prediciton width, one can specify the quantiles. so width=.95 is equivalent to quantiles=[.025, .975]. if None, defaults to width.
- meshgrid (bool, whether to return and accept meshgrids.) –
Useful for creating outputs that are suitable for 3D plotting.
Note, for simple terms with no interactions, the output of this function will be the same for
meshgrid=Trueandmeshgrid=False, but the inputs will need to be different.
Returns: - pdeps (np.array of shape (n_samples,))
- conf_intervals (list of length len(term)) – containing np.arrays of shape (n_samples, 2 or len(quantiles))
Raises: ValueError : – If the term requested is an intercept since it does not make sense to process the intercept term.
See also
generate_X_grid()- for help creating meshgrids.
-
predict(X)¶ preduct expected value of target given model and input X often this is done via expected value of GAM given input X
Parameters: X (array-like of shape (n_samples, m_features)) – containing the input dataset Returns: y – containing predicted values under the model Return type: np.array of shape (n_samples,)
-
predict_mu(X)¶ preduct expected value of target given model and input X
Parameters: X (array-like of shape (n_samples, m_features),) – containing the input dataset Returns: y – containing expected values under the model Return type: np.array of shape (n_samples,)
-
sample(X, y, quantity='y', sample_at_X=None, weights=None, n_draws=100, n_bootstraps=5, objective='auto')¶ Simulate from the posterior of the coefficients and smoothing params.
Samples are drawn from the posterior of the coefficients and smoothing parameters given the response in an approximate way. The GAM must already be fitted before calling this method; if the model has not been fitted, then an exception is raised. Moreover, it is recommended that the model and its hyperparameters be chosen with gridsearch (with the parameter keep_best=True) before calling sample, so that the result of that gridsearch can be used to generate useful response data and so that the model’s coefficients (and their covariance matrix) can be used as the first bootstrap sample.
These samples are drawn as follows. Details are in the reference below.
1.
n_bootstrapsmany “bootstrap samples” of the response (y) are simulated by drawing random samples from the model’s distribution evaluated at the expected values (mu) for each sample inX.2. A copy of the model is fitted to each of those bootstrap samples of the response. The result is an approximation of the distribution over the smoothing parameter
lamgiven the response datay.3. Samples of the coefficients are simulated from a multivariate normal using the bootstrap samples of the coefficients and their covariance matrices.
Notes
A
gridsearchis donen_bootstrapsmany times, so keepn_bootstrapssmall. Maken_bootstraps < n_drawsto take advantage of the expensive bootstrap samples of the smoothing parameters.Parameters: - X (array of shape (n_samples, m_features)) – empirical input data
- y (array of shape (n_samples,)) – empirical response vector
- quantity ({'y', 'coef', 'mu'}, default: 'y') – What quantity to return pseudorandom samples of. If sample_at_X is not None and quantity is either ‘y’ or ‘mu’, then samples are drawn at the values of X specified in sample_at_X.
- sample_at_X (array of shape (n_samples_to_simulate, m_features) or) –
- optional (None,) –
Input data at which to draw new samples.
Only applies for quantity equal to ‘y’ or to ‘mu’. If None, then sample_at_X is replaced by X.
- weights (np.array of shape (n_samples,)) – sample weights
- n_draws (positive int, optional (default=100)) – The number of samples to draw from the posterior distribution of the coefficients and smoothing parameters
- n_bootstraps (positive int, optional (default=5)) – The number of bootstrap samples to draw from simulations of the response (from the already fitted model) to estimate the distribution of the smoothing parameters given the response data. If n_bootstraps is 1, then only the already fitted model’s smoothing parameter is used, and the distribution over the smoothing parameters is not estimated using bootstrap sampling.
- objective (string, optional (default='auto') – metric to optimize in grid search. must be in [‘AIC’, ‘AICc’, ‘GCV’, ‘UBRE’, ‘auto’] if ‘auto’, then grid search will optimize GCV for models with unknown scale and UBRE for models with known scale.
Returns: draws – Simulations of the given quantity using samples from the posterior distribution of the coefficients and smoothing parameter given the response data. Each row is a pseudorandom sample.
If quantity == ‘coef’, then the number of columns of draws is the number of coefficients (len(self.coef_)).
Otherwise, the number of columns of draws is the number of rows of sample_at_X if sample_at_X is not None or else the number of rows of X.
Return type: 2D array of length n_draws
References
Simon N. Wood, 2006. Generalized Additive Models: an introduction with R. Section 4.9.3 (pages 198–199) and Section 5.4.2 (page 256–257).
-
score(X, y, weights=None)¶ method to compute the explained deviance for a trained model for a given X data and y labels
Parameters: - X (array-like) – Input data array of shape (n_samples, m_features)
- y (array-like) – Output data vector of shape (n_samples,)
- weights (array-like shape (n_samples,) or None, optional) – Sample weights. if None, defaults to array of ones
Returns: explained deviancce score
Return type: np.array() (n_samples,)
-
set_params(deep=False, force=False, **parameters)¶ sets an object’s paramters
Parameters: - deep (boolean, default: False) – when True, also sets non-user-facing paramters
- force (boolean, default: False) – when True, also sets parameters that the object does not already have
- **parameters (paramters to set) –
Returns: Return type: self
- terms (expression specifying terms to model, optional.) –